Dibujo tecnico

Nicole López Consuegra 2°A ESO
 

1° trimestre 

dibujo de paralelas con escuadra y cartabón



 Paso 1: coloca la escuadra sobre el papel y traza una recta (preferiblemente por el lado más amplio de la escuadra).

Paso 2: Coloca el cartabón junto a la escuadra como aparece en el dibujo siguiente, con mucho cuidado de que esta no se mueva.

Paso 3:Ahora debes sujetar firmemente el cartabón y deslizar la escuadra para trazar las paralelas.

dibujo de paralelas con compás
https://www.youtube.com/watch?v=nosS8NBU19A


dibujo de perpendiculares con escuadra y cartabón


Paso 1: Coloca la escuadra y el cartabón del mismo modo que para trazar paralelas (ver imagen anterior de trazado de paralelas).

Paso 2: traza una recta.

Paso 3: sujeta el cartabón y gira la escuadra hasta cambiar su lado de apoyo sobre el cartabón (ver la viñeta 4).

Paso 4: desliza la escuadra sobre el cartabón hasta conseguir la posición donde deseas trazar la perpendicular (ver la viñeta 5).

Paso 5: traza la recta perpendicular.

dibujo de perpendiculares con compás
https://www.youtube.com/watch?v=h3KwJyoRye0

 mediatriz
https://www.youtube.com/watch?v=QNrQCT9N6rQ

Dado el segmento AB, para dibujar su mediatriz se procede de la siguiente forma:

Paso 1: Con centro el punto A trazar un arco, como muestra la figura de la derecha.

Paso 2: Con la misma abertura del compás trazar otro arco desde el punto B.

Paso 3: Unir con una regla los puntos de corte de los dos arcos, como muestra la figura.

La recta trazada es la MEDIATRIZ del segmento AB que lo corta en su punto medio M.

Este procedimiento puede usarse para encontrar el punto medio de un segmento

pasar ángulos

 https://www.youtube.com/watch?v=kTwCrVDMaIg

• En el primer arco trazamos un arco cualquiera que nos da los puntos A y B.

• Trasladamos el punto A trazando un arco igual en el nuevo vértice.

• Trasladamos con otro arco la distancia AB, identificando el punto B del nuevo ángulo.

suma y resta de ángulos 
 https://www.youtube.com/watch?v=aVr0pLUvJPY

Para sumar o restar dos ángulos, basta poner uno a continuación del otro. Para sumarlos se dibujan los dos en el mismo sentido compartiendo el vértice, y para restarlos se dibujan en sentido contrario.

Por convención, los ángulos positivos se cuentan en el sentido de giro anti horario, y los negativos en el sentido contrario.



bisectriz
 https://www.youtube.com/watch?v=DWh2GSa6GSA

La bisectriz de un ángulo es la recta que pasando por el vértice del ángulo lo divide en dos ángulos iguales.

Trazar la bisectriz

1 Se traza un arco correspondiente al ángulo
2 Desde los dos extremos del arco trazado se trazan, con cualquier abertura del compás, dos arcos que han de cortarse en un punto.
3 La bisectriz se obtiene dibujando la recta que une ese punto con el vértice.


teorema de Tales
https://www.youtube.com/watch?v=dqWRtHWI0-c 




TRIANGULOS:

clases de triangulos:

Un triángulo es un polígono que tiene tres lados, tres ángulos y tres vértices. 
Es el polígono con menor número de lados.
Una propiedad fundamental del triángulo es que la suma de sus ángulos siempre es 180º.

Los triángulos se clasifican normalmente según el tipo de ángulos que tiene o según sus lados.
Según sus lados:

• Triángulo equilátero:
  • Los tres lados son iguales.
  • Los ángulos también son iguales y miden exactamente 60º.
• Triángulo isósceles:
  • Dos de sus lados son iguales.
  • Dos de sus ángulos son iguales.
• Triángulo escaleno:
  • Ningún lado es igual.
  • Ningún ángulo es igual.

Según sus ángulos:

• Triángulo acutángulo: sus tres ángulos son agudos, menores de 90º
• Triángulo rectángulo: Tiene un ángulo recto y los otros dos son agudos.
  • El lado mayor de un triángulo rectángulo se llama hipotenusa.
  • Los otros dos lados se llaman catetos.

Triángulo obtusángulo: tiene un lado obtuso, mayor de 90º.   



construcción de triángulos: 

construcción de un triángulo equilátero dado el lado:
https://www.youtube.com/watch?v=_0Fv7RSHx4w 

---

1. Sobre un lugar determinado por nosotros (es posible que en algún caso, nos pidan construir en un sitio concreto), se situa el lado a del triángulo equilátero, que nos dan como dato.
Aunque no es necesario, es preferible que este lado esté sobre la línea horizontal, es decir, paralela a los márgenes inferior y superior de la lámina.

.
2. Desde uno de los extremos del lado a, por ejemplo, el punto C, se traza un arco con la medida del lado a. Lógicamente tiene que pasar por el punto B.
.
.
.
3. Se realiza la misma operación desde el otro extremo, el punto B. Obtenemos otro arco que pasa por el punto C y que corta al anterior en el punto A.
Los tres puntos (A, B y C) forman los tres vértices del triángulo equilátero.
.
4. Se repasan los tres lados a, b y c, uniendo los tres vértices: A, B y C, y tenemos el triángulo equilátero que nos pedían.



construcción de un triángulo equilátero dado el radio:
https://www.youtube.com/watch?v=LjydWhu2QOI 

Tracemos un diámetro a la circunferencia orientado verticalmente. Éste cortará a la circunferencia en A y N.

Con el radio de la circunferencia y haciendo centro en N, trazamos un arco que nos cortará a la circunferencia en B y C. Uniendo A, B y C trazamos el triángulo equilátero inscrito en la circunferencia de radio dado. 

construcción de un triángulo isósceles  dado los lados:
 https://www.youtube.com/watch?v=0uJF1IOwCV4



1. Seleccionamos uno de los lados para la primera operación, por ejemplo el lado c, lado desigual.
Colocamos este lado en el lugar donde vayamos a trabajar. Este lugar me lo pueden dar determinado o bien puede ser un lugar que libremente establezcamos nosotros.
.
En este caso, trazamos una recta r cualquiera y sobre un punto A cualquiera, se traza un arco con la medida del lado c.
Queda situado el lado c con sus vértices A y B.
.
2. Desde el vértice B y con la medida del lado a, se traza un arco.

.
3. Se realiza la misma operación trazada anterioremente pero, en este caso, desde el vértice A y con el lado b (que es igual al lado a).

.
.
.

.Los dos arcos se cortan en el vértice C, formando de esta forma el triángulo isósceles.
.

.
.
4. Uniendo los tres vértices: A, B y C, obtenemos el triángulo construido con los tres lados a, b y c.
.
.
5. Se repasan los tres lados a, b y c, uniendo los tres vértices: A, B y C, y tenemos el triángulo que nos pedían. SOLUCIÓN.

 

 construcción de un triángulo escaleno dado 2 lados:
https://www.youtube.com/watch?v=z1PzH1P-SOU

construcción de un triángulo rectángulo dado la hipotenusa y el cateto:
https://www.youtube.com/watch?v=1KKkq4vlVeE


CUADRILÁTEROS:
  
Un cuadrilátero es un polígono con cuatro lados.
Hay muchos tipos especiales de cuadriláteros.
Un paralelogramo es un cuadrilátero en que ambos pares de lados opuestos son paralelos .

Un paralelogramo también tiene las siguientes propiedades:

• Los ángulos opuestos son congruentes;
• Los lados opuestos son congruentes;
• Los ángulos adyacentes son suplementarios;
• Las diagonales se bisectan una con otra.

Un rectángulo es un paralelogramo con cuatro ángulos rectos, así todos los rectángulos también son paralelogramos y cuadriláteros. Por otro lado, no todos los cuadriláteros y paralelogramos son rectángulos.

Un rectángulo tiene todas las propiedades de un paralelogramo, más la siguiente:

• Las diagonales son congruentes.

 
Un rombo es un paralelogramo con cuatro lados congruentes . El plural de rombo es rombos . (Amo esa palabra.)

Un rombo tiene todas las propiedades de un paralelogramo, más la siguiente:

• Las diagonales se intersectan en ángulos rectos.

Un cuadrado puede ser definido como un rombo que también es un rectángulo – en otras palabras, un paralelogramo con cuatro lados congruentes y cuatro ángulos rectos.

Un trapezoide es un cuadrilátero con exactamente un par de lados paralelos. (Puede haber alguna confusión con esta palabra dependiendo en que país se encuentre. En la India y Bretaña, ellos le dicen trapecio ; en América, trapecio usualmente significa un cuadrilátero sin lados paralelos.)

Un trapezoide isósceles es un trapezoide cuyos lados no paralelos son congruentes.

Construcción de cuadriláteros:

Cuadrado inscrito en una circunferencia de radio conocido
https://www.youtube.com/watch?v=CJ6B9ubTeAY&t=34s

Construcción de Cuadrado Inscrito en una Circunferencia, sabiendo que AB es una de sus diagonales. Para realizar esta actividad debemos seguir los siguientes pasos: 

1. Trazar un segmento AB .

2. Obtener el punto medio del segmento medio AB, a través de la herramienta punto medio o centro.

3.Trazamos la recta perpendicular al segmento AB haciendo click sobre el punto medio y el segmento AB, a través de la herramienta perpendicular. 

4.Dibujamos la circunferencia (centro-punto), haciendo click sobre el segmento A y el centro; a través de la herramienta circunferencia (centro-punto). 

5. Se debe nombrar los puntos de intersección entre la circunferencia y la recta perpendicular D y E. 

6. Utilizando la herramienta polígono; hacer click sobre los puntos A,D,B, C y por último sobre A, de esta forma se dibujara el cuadrado.

Rectángulo conociendo la diagonal y un lado
https://www.youtube.com/watch?v=iDgLeGuK76o

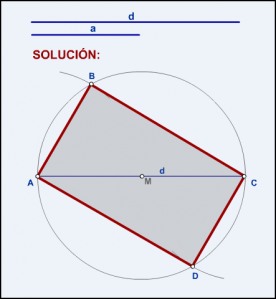
1. Se coloca la diagonal d (segmento AB) sobre una recta cualquiera r.
2. Se halla el punto medio M de la diagonal y se traza una circunferencia que pase por sus extremos (puntos A y C).
3. Desde A y C se trazan dos arcos de radio a.
4. Se unen los puntos hallados (B y D), con los extremos de la diagonal (A y C) y se obtiene el rectángulo.

Rombo conocidas las diagonales
https://www.youtube.com/watch?v=v0oaBu3VnA4

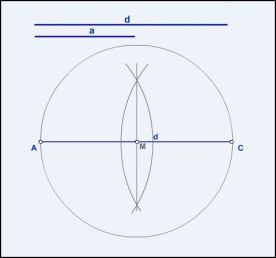
1. Se coloca la diagonal sobre una recta r cualquiera. Se obtienen los puntos A y C.
2.  Con el lado a como radio, se trazan dos arcos desde A y C. Obtenemos los puntos B y D.
3. Se unen los extremos de la diagonal (A y C) con los puntos hallados (B y D) y se obtiene el rombo.

Trapecio rectángulo conocidas las bases y la altura
https://www.youtube.com/watch?v=xntnlS95Gv4

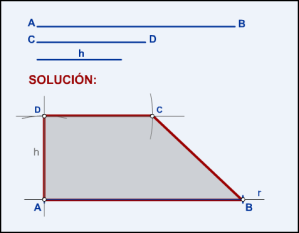
1. Sobre una recta r cualquiera se coloca la base AB.
2. Se traza una perpendicular a AB en uno de sus extremos (por ejemplo en A) y se lleva la altura h.
3. Por D se traza una paralela a AB y se lleva la base superior CD.
4. Se unen los puntos A, B, C y D y se obtiene el trapecio recto.

CONSTRUCCIÓN DE POLÍGONOS REGULARES:

 Método general
https://www.youtube.com/watch?v=_0vOjP5Wfm4&t=3s

1.Trazar el diámetro AB.

2.Con centro en A y B trazar arcos de radio AB,
la intersección es el punto X.

3.Dividir el diámetro AB en n partes.

4.Desde X trazar la recta que pasa por 2 hasta la circunferencia.

5.Con Ln determinado, llevamos con el compás el lado del polígono sobre la circunferencia, por la derecha y por la izquierda.

 CONSTRUCCIÓN DE POLÍGONOS ESTRELLADOS:

 Polígonos estrellados
https://www.youtube.com/watch?v=281XAjZsYmg